定常と非定常
時間的に変化しない流れを定常流(steady flow),変化する流れを非定常流(unsteady flow)という。非定常流の解析は難しく、多少の時間的な変化であれば定常流として扱う場合が多い。
(流体の)質量保存の法則
流管を横切る流れはないとし、また定常流を仮定すると流管の形は変化しないことになる、質量保存の法則から、このような流管に沿った2点A、Bでの単位時間に通過する質量は変わらないので、次式が成立する。
(流体の)エネルギー保存の法則
ベルヌーイの定理、密度一定で外力が重力のみの定常流において、一つの流線に沿って、粘性摩擦によるエネルギー損失がないとき、次式が成り立つPA,PB〔Pa〕はそれぞれ点A、Bでの圧力、vA,vB〔m/s〕は速度を表す。単位体積当り第1項は圧力として貯えられるエネルギ、第2項は運動エネルギ表す。よって,式はエネルギ保存則を示しており,これをベルヌーイの定理(Bernoulli’s theorem)という。
差圧式流量計
図のように管路内に絞り(オリフイス:orifice)がある場合に、絞り前後の断面でベルヌーイの定理を適用する。ここで管断面での流速は一定であると仮定するとP1、v1 、P2 、v2 は、それぞれ断面A、Bでの圧力と流速で,ρ 〔kg/m3〕は流体の密度また断面A、Bの断面積をS1 , S2 とすると容積流量Q〔m3/s〕はとなる。断面A、Bの差圧から流量が求められるので、差圧式流量計(differential flow meter)と呼ばれる。実際には縮流の影響で、S2は絞りの断面より小さく,また粘性の影響などにより、修正することが必要となる。絞りの直径d を用いてつぎのように表す。αは流量係数(flow coefficient)と呼ばれる。圧縮性流体である気体を測定する場合には、さらに修正が必要で、つぎの様にあらわされる。ここで、εは圧縮係数とよばれる。一般に、絞り部としてはオリフイス以外に図に示すノズル(nozzle)やベンチユリ管(Venturi tube)が用いられ、標準の絞り部ではαとεの値はJISで決められた規格値を利用することができる。
面積式流量計
差圧式流量計は絞り部の断面積を一定にし,前後の差圧から流量を求めるのに対し、面積式流量計(areal flow meter)は差圧を一定とし、絞り面積の変化割合から流量を求める。面積式流量計の代表的なものはフロート式で、図に示すようにテーパ管の中にフロートがあり、流体は下から上に流れる構成になっている。従って、流体はテーパ管とフロートの隙間を流れるため、流量が増加するとフロートは上昇し、隙間の大きさを拡大する。テーパ管に付けられた目盛から流量を読み取る。フロート前後の圧力をP1、P2フロートの体積、断面積をVf、Sf とすると次式が成立する。ρf、ρ、gはそれぞれフロート,流体の密度,そして重力加速度である。また,流量Qは原理的に差圧式流量計式と同様に,隙間の断面積をSgとすると次式の様に表わされる。流量係数αはテーパ管の断面形状,フロートの形状、レイノルズ数に依存する。
容積式流量計
回転の都度交互に、一定容積の流体を移送する構造で、回転数によって流量の積算量を表すことができる。

こんにちは。
今日もものづくりの勉強をしていきたいと思います。今日は流量の測定ということについて学習していきたいと思います。今日のお話を聞いてくれるといろいろな場所で使われている流量計の原理が分かるようになります。簡単に自己紹介すると私は日本がものづくりの国だというふうに考え男性女性理系文系問わずものづくりの知識をみんなが身につければ日本がもっといいものづくりをできる国になるなのではないかと考え情報発信をしています。では、流量の測定ということで学習していきたいと思います。

今日は次のような順序で話をしていきたいと思います。最初は差圧流量計というものについて学習していきます。次に面積流量計というものについて学習していきます。3番目に容積流量計というものについて学習していきます。

最初に、流れには定常と非定常と言われる状態があります。変化しない流れのことを定常流とよび、変化する場合は非定常流という風にいいます。多少の変化であれば定常流として取り扱う場合が多くあります

なぜ、定常流の話をしたかと言うと次に言う質量保存の法則というのを考えないと差圧流量計の説明がすることができないからです。定常流なら次に示す質量保存というのが成立することになります。質量保存というのは例えば 配管の中の断面積が変化しても変化するのは質量ではなくて流体の速度になります。つまりここに書いてある式のようにρを密度、vを速度とするとある断面積 A の場所とある断面積 B の場所は異なる面積ですが、その場合のρvAの積は常に一定ということになります。この理屈が使われている場面あるいはこの理屈を身近に感じることはできる場面としてホースの先端を押しつぶすと先端の断面積が小さくなる代わりに水の速度が上がって水が勢いよくホースから出ていくというのがあります。

次に流体のエネルギー保存の法則というのを考えていきます。摩擦による損失がないとする時に次の式が成立します。次の式というのはある地点Aとある地点B、それぞれ配管内の断面積が異なる場所を表していますがその場所における静圧PAと動圧1/2 ρVAの二乗はBの位置における静圧と動圧の和に等しいという関係がエネルギー保存の法則になります。ここで PA、PB はそれぞれ上流下流での圧力、va、vbはそれぞれの位置の速度を表します。エネルギー保存を表すこの式をベルヌーイの定理という風に言います
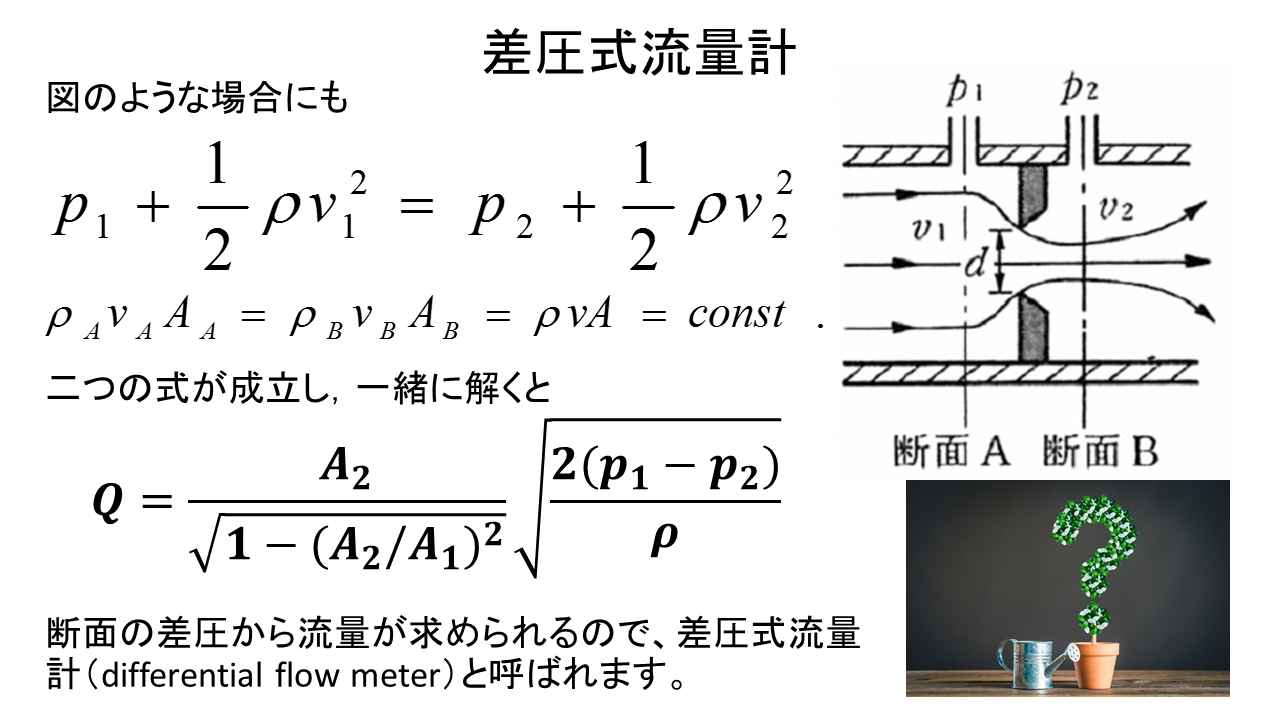
次に差圧流量計の説明をしていきます。この図に示すように配管内の流量を知りたい場合にはこのオリフィスとよばれる五円玉のような形をしたものを配管内に挿入し意図的に断面積が小さい領域を作ってあげることになります。そうするとこの断面積が小さくなっている部分とそうでない部分について先ほど述べたエネルギー保存の法則と質量保存の法則が成立するので二つの式を連立すると次のような式が出てきます。配管の断面積A1と意図的に縮流させたオリフィスの断面積A2では管内を流れる流体の密度はρ、縮流する前の流体の静圧はp1、縮流部に発生する流体の静圧p2になります。従って管内の静圧と縮流部の静圧の差を圧力計によって計測することにより、配管の断面積A1、A 2、密度にしても分かっていますので流量 Q を知ることができます。配管内の差圧から流量が求められるので差圧式流量計、ディファレンシャルフローメーターと呼ばれます。
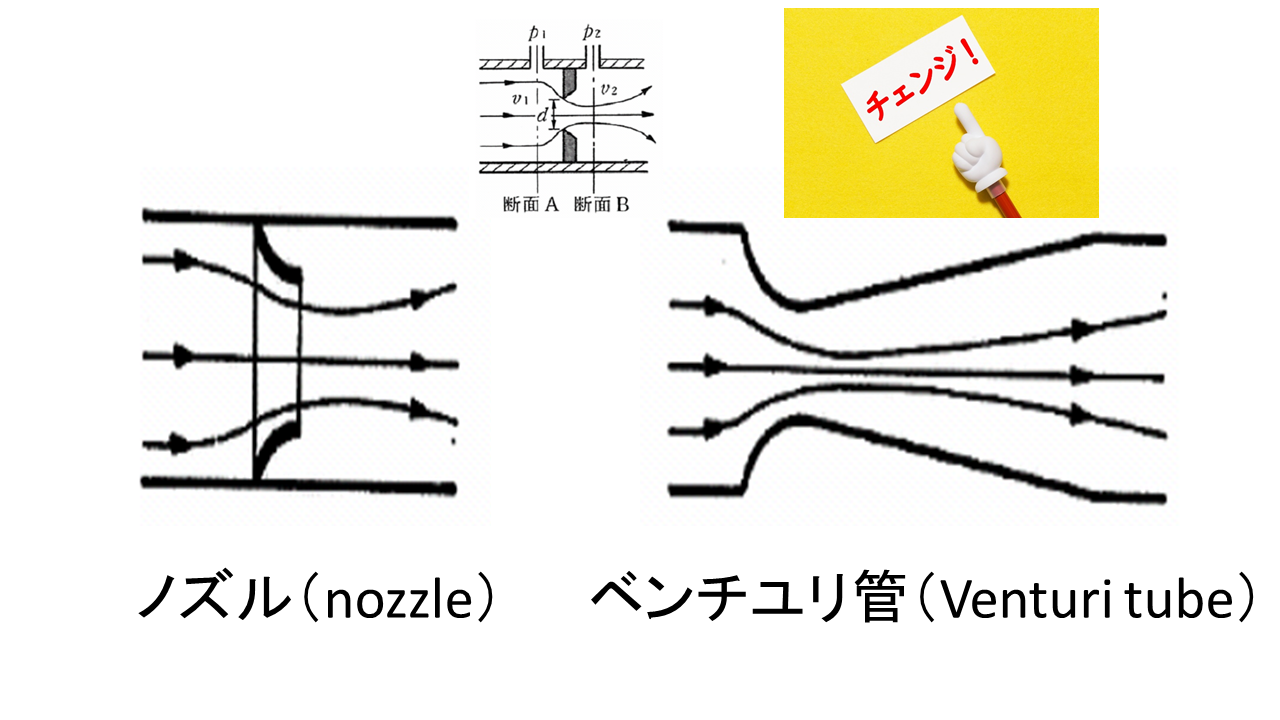
先ほどを管内の流量を測定するために縮流部を設ける必要があるということを言いました。しかしながらこのオリフィスと呼ばれる縮流部は見るからに缶の中で流体の抵抗となり配管内の圧力損失を増やすということが予想されます。従ってオリフィスよりも圧力損失が少ない宿流部として次のようなノズルですとかあるいはベンチュリーというのを配管内に挿入する場合もあります。しかしながらノズルあるいはベンチュリーになるに従って圧力損失は小さいですが設置のコストは上がるという特徴があります

次に面積式流量計について考えていきたいと思います。面積式流量計の構造はこの図のようになっていてテーパー管と呼ばれる徐々に太くなる缶の中にフロートが入れてあります。フロートは、通常では一番下に下がっているのですがこのテーパー管にある流量 Q が流れるとその流量に比例します。流量Qに比例してフロートの位置が上に上がっていくためにこのフロートの平らな部分と横についている目盛りの一致する位置を読むと現在の流量を知ることができるというのが面積式流量計の原理になります。
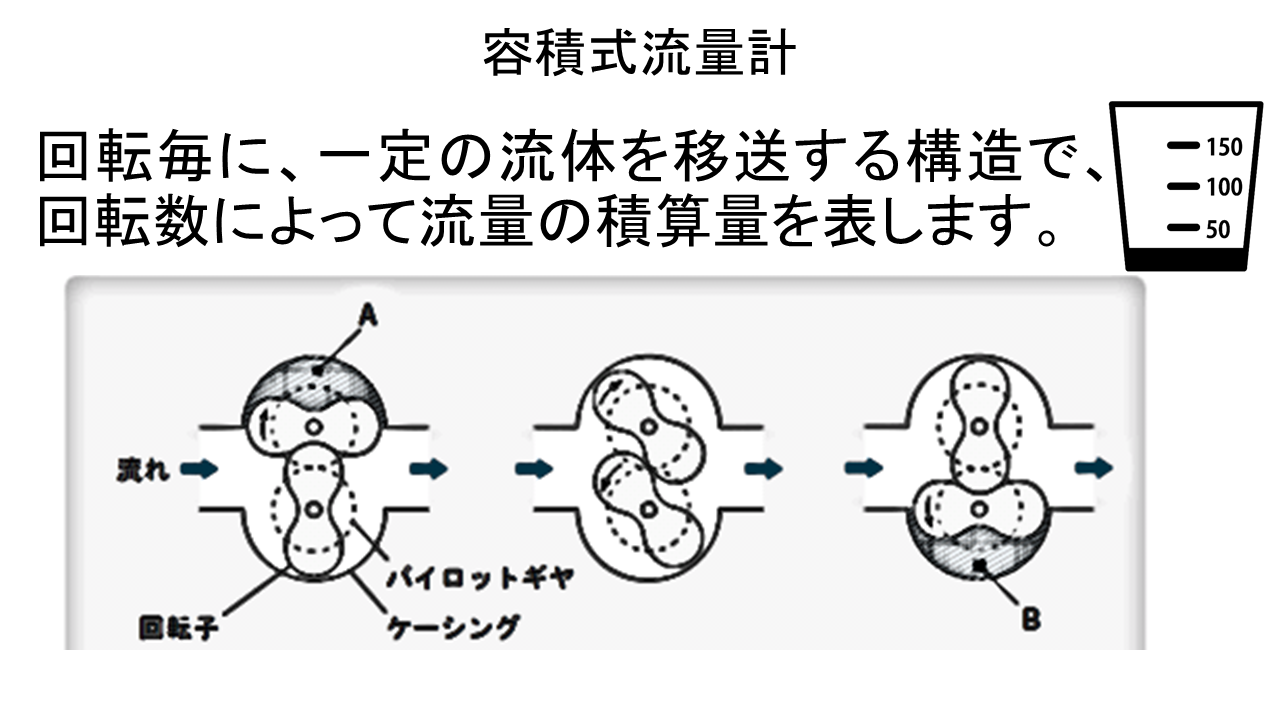
容積式流量計の原理はここにあるビーカーで一杯二杯という感じで液体の量を測っていくようなものになります。それを連続的に行うためにこの図のような回転するひょうたんのような形をした回転子を二つ使って回転子が作り出す隙間の容積が回転するごとに入れ替わるので回転数、つまり回転数かける隙間の容積がこの部分を通り抜けていった液体の量になるのでこのひょうたん型が回転する回数からこの流量計を通り抜けた液体の流量を知ることができます







